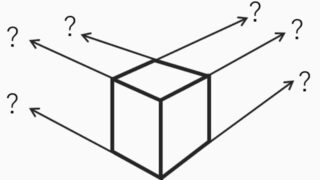
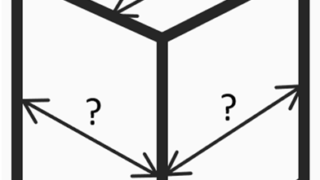
こんにちはカクシュウです!
【必読3】ではそれぞれの角度に関係に注目して
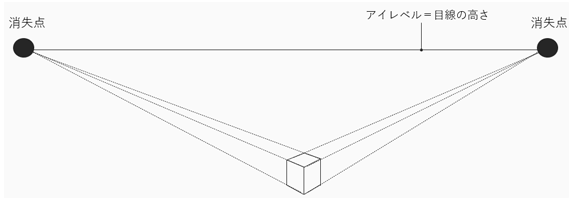
消失点が画面外にあっても、だいたい正確に消失点に向かわせる
方法をご紹介いたしました。
【必読3】画面外に消失点があるとパースが狂ってしまう!→角度の関係に気づけば描けます!|角度でわかる!二点透視図法克服法 (kakusyu.com)
実は、今回紹介する様な角度の関係になると
上手く描けなくなります。
なので、今回はその対処方法をご紹介します。
どのような角度の関係かといいますと、
【必読1】で紹介した、
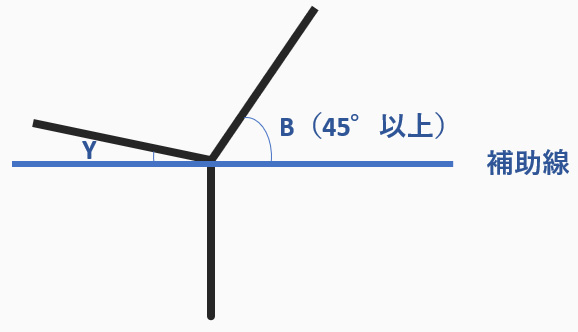
角B+角Y<90°を満たしていても
角B、角Yどちらかが45°以上
になる場合です。
【必読1】2点透視図法わかりづらい!→まずこの1点だけわかれば大丈夫!|角度でわかる!二点透視図法克服法 (kakusyu.com)
なぜ上手く描けなくなるのか、
実際にこのシチュエーションで【必読3】の方法を
用いて描いてみましょう。
下図のように、だいたいになりますが、角Bを45°以上に設定します。
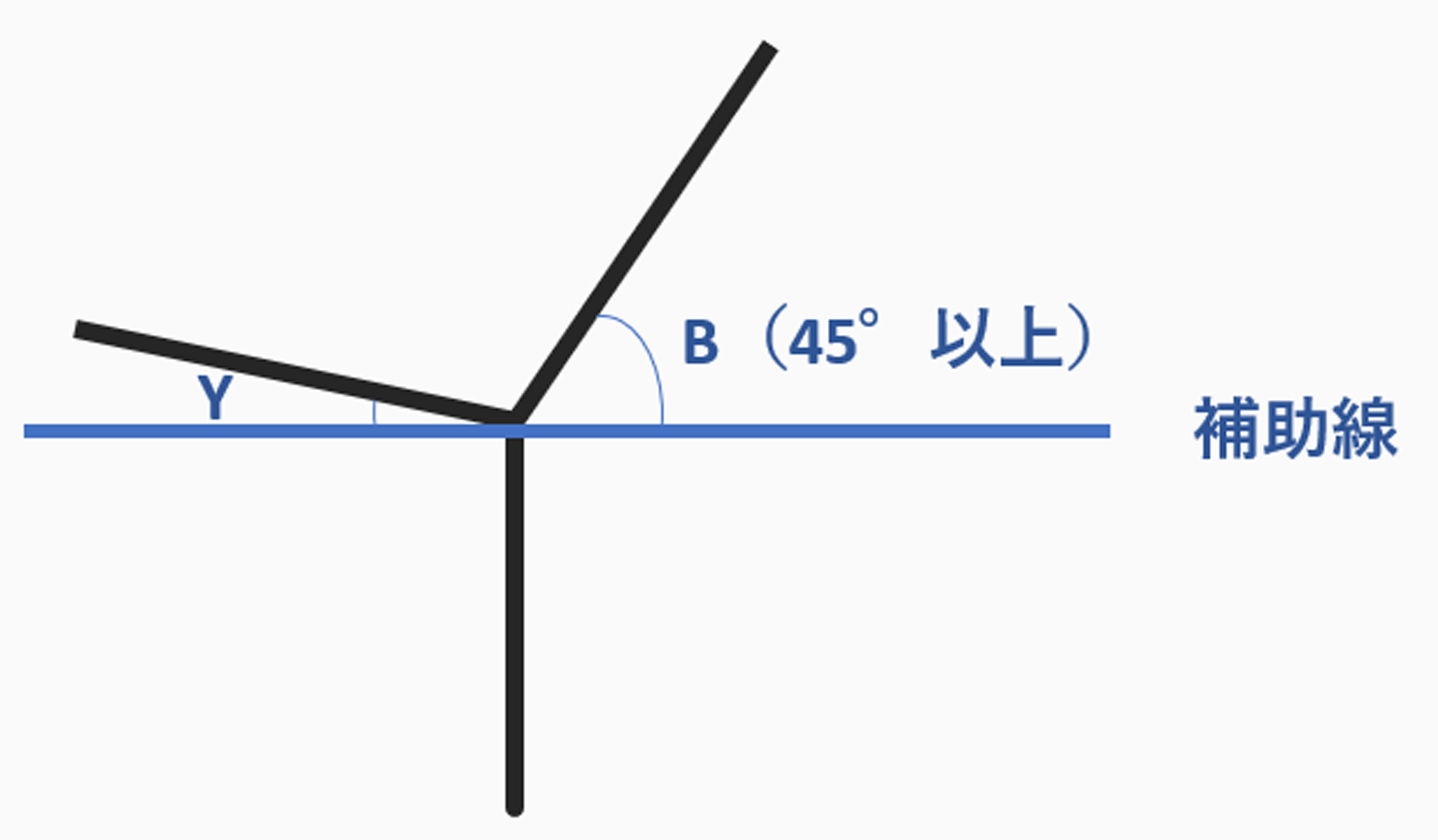
【必読3】の方法を用いて角Bの2倍になるように、
角Cを決めてみます。
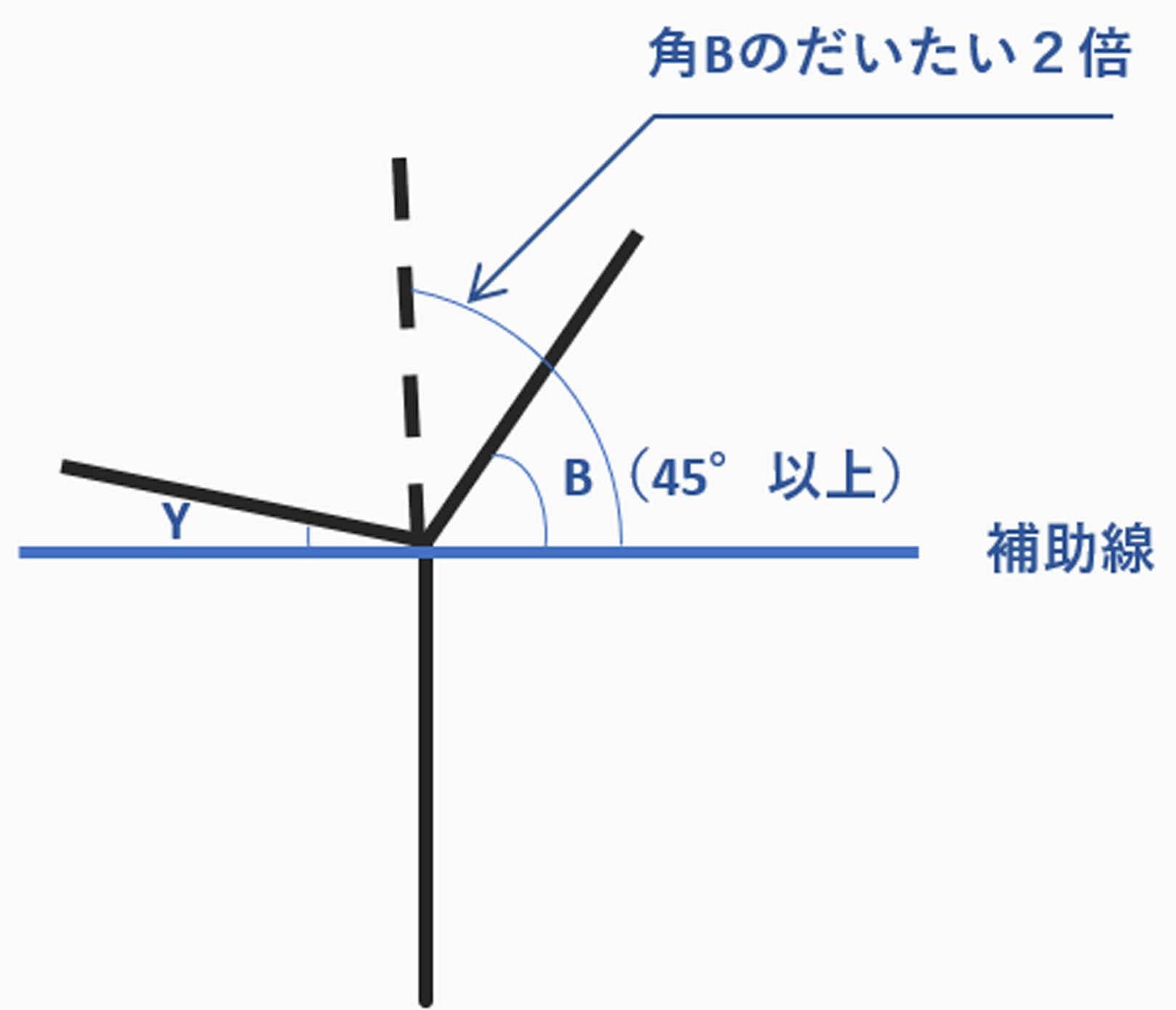
この時点で何かお気づきでしょうか?
この状態で角Cを作成すると、
明らかに消失点に向かわず、
パースを成立させるのが、明らかに無理なのが
わかります。
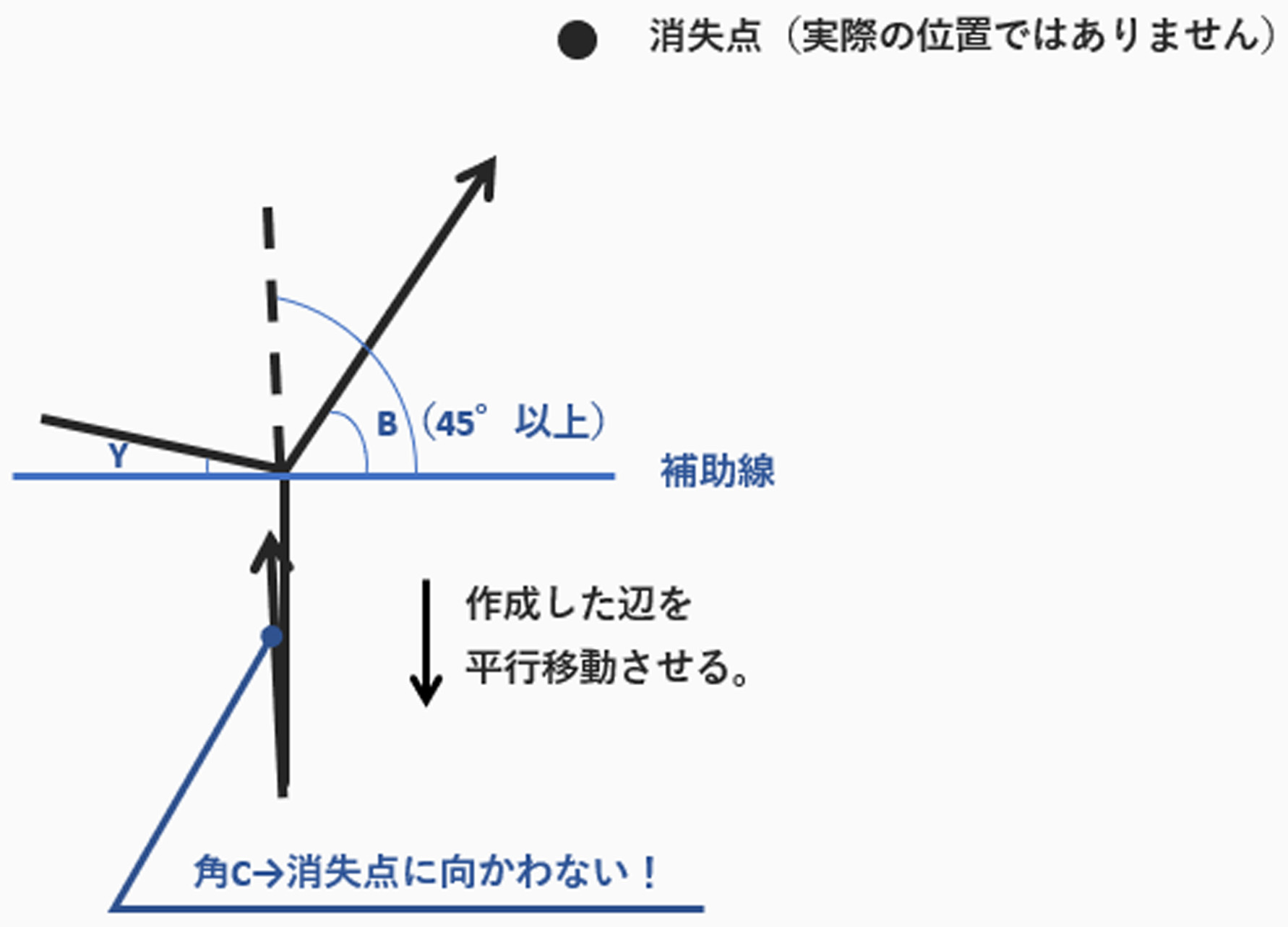
このような状態ではどうしたらいいのでしょうか?
キーワードは

です。
「何のこっちゃ?」と思う方が多々おられると
思いますが、このキーワードを元に、先程の
パースが成立しない関係を修正してみましょう!
先程、角Bを2倍で作成した角Cを
2倍の半分で作成します。
文章で説明すると分かりづらいですが
図のように、2倍で作成したものを半分にします。
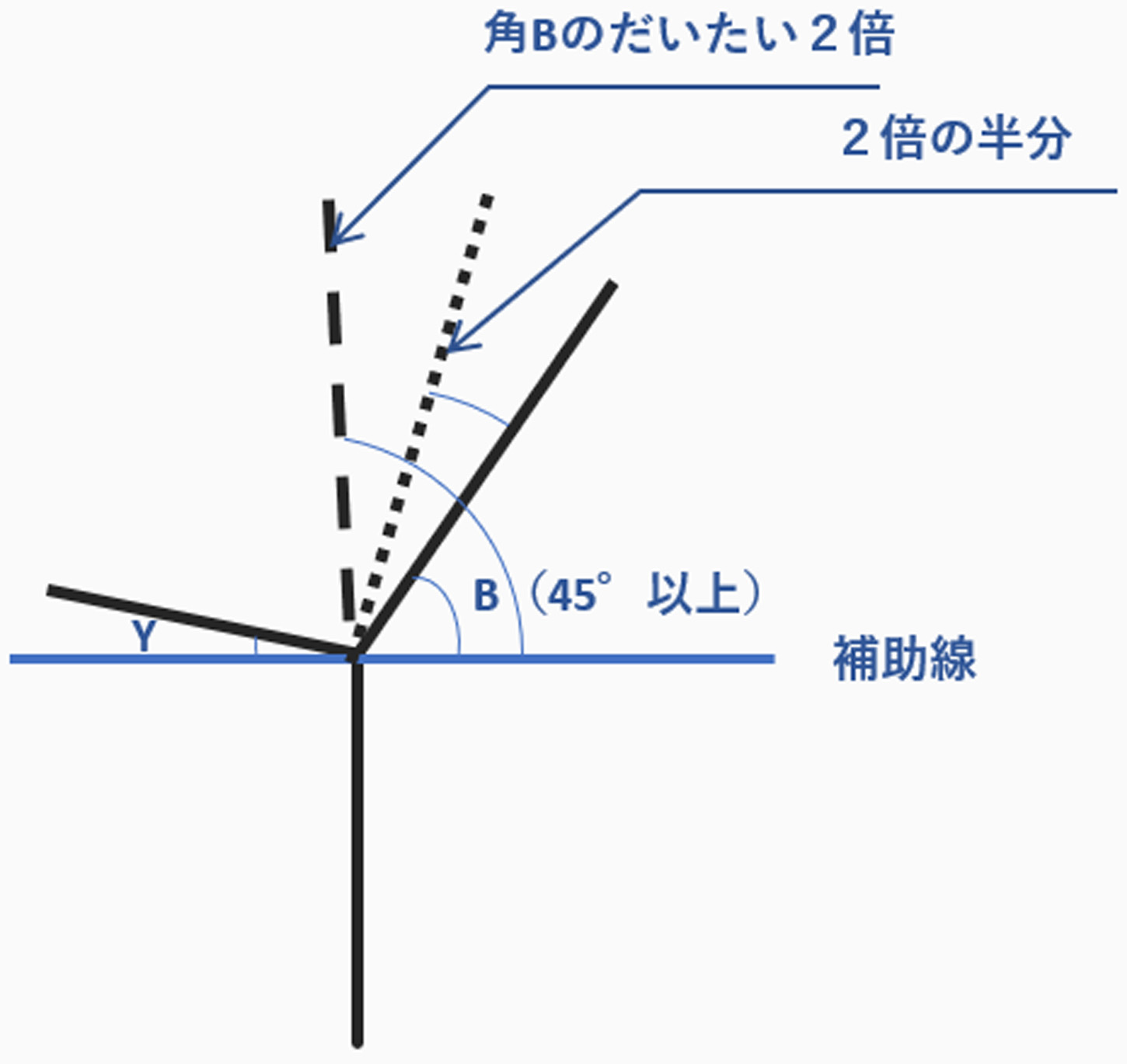
これを平行移動して、角Cを作成します。
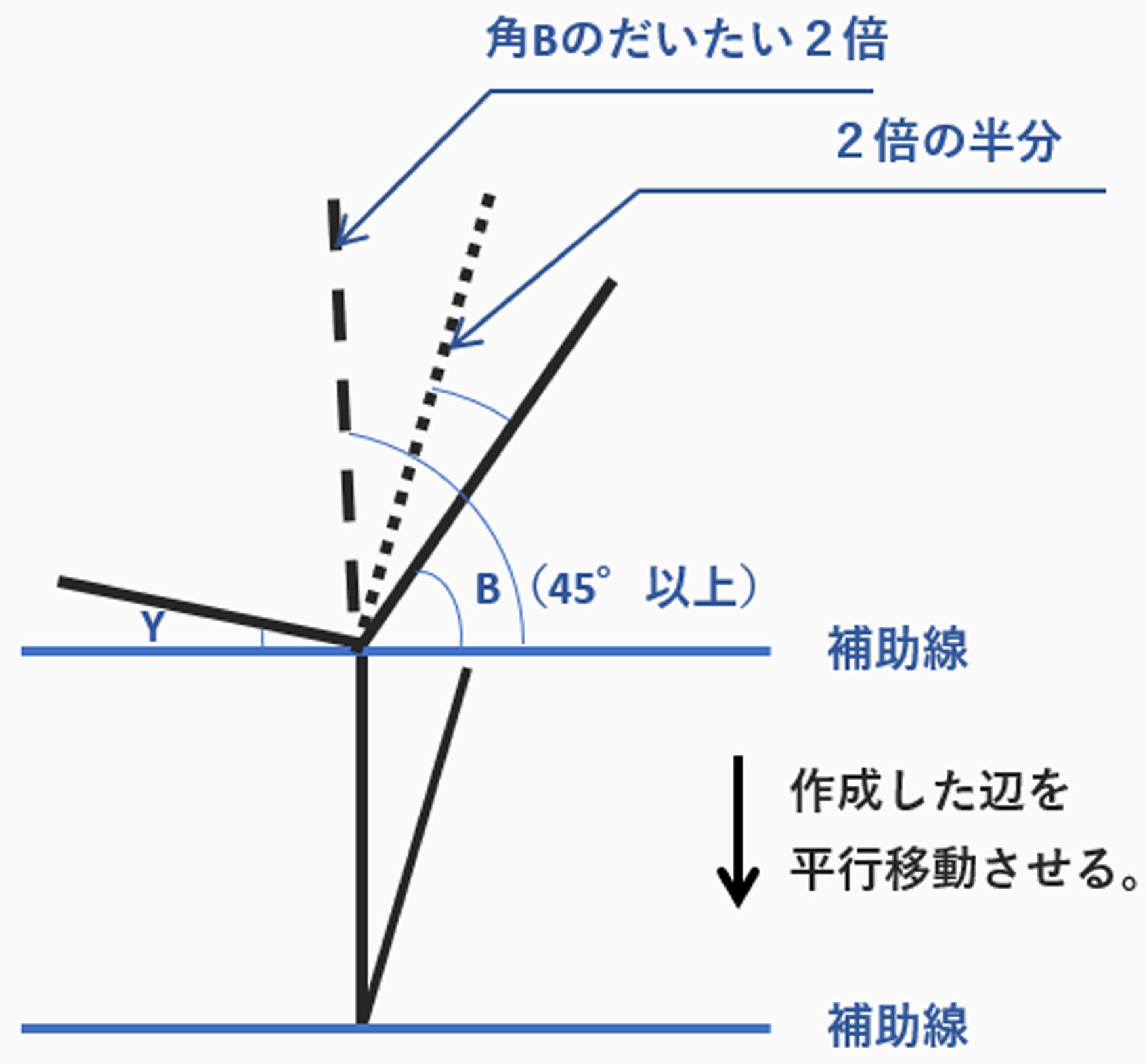
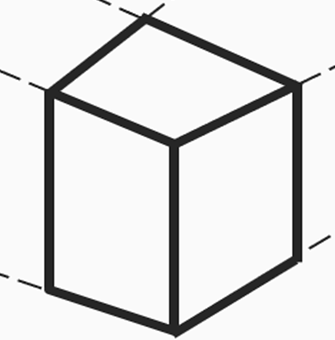
これを元に立方体を作成します。
角C以外の角度の関係は【必読3】でお伝えした
関係と同じです。
【必読3】画面外に消失点があるとパースが狂ってしまう!→角度の関係に気づけば描けます!|角度でわかる!二点透視図法克服法 (kakusyu.com)
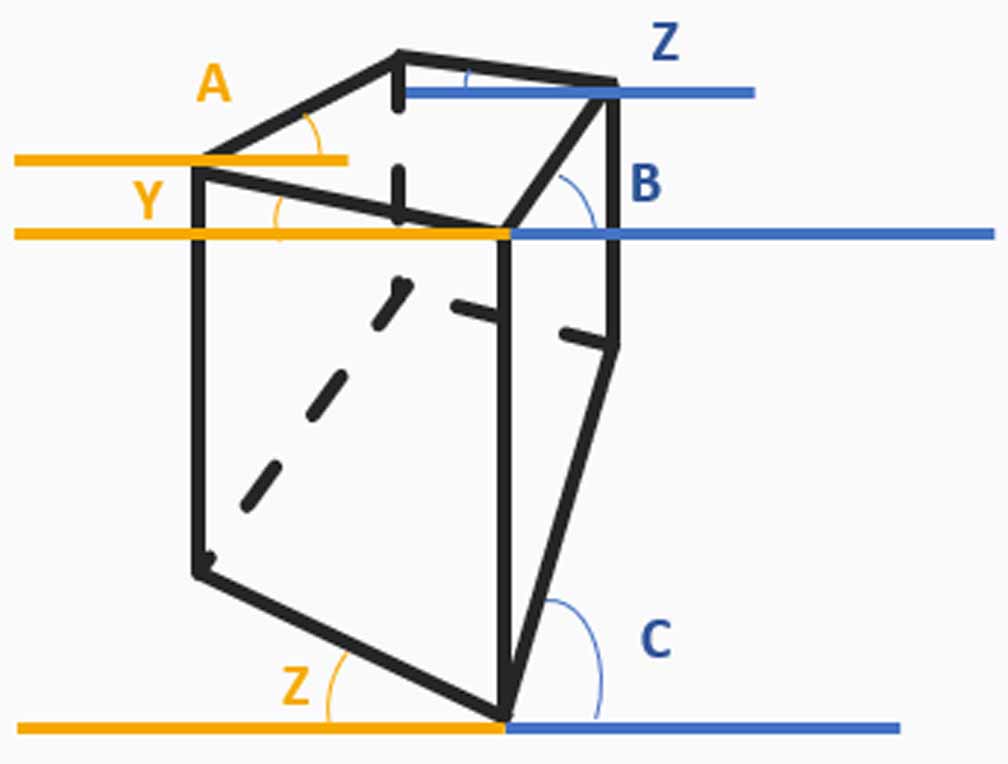
試しに、それぞれの辺を延長させて
消失点に向かっているか確認してみましょう。
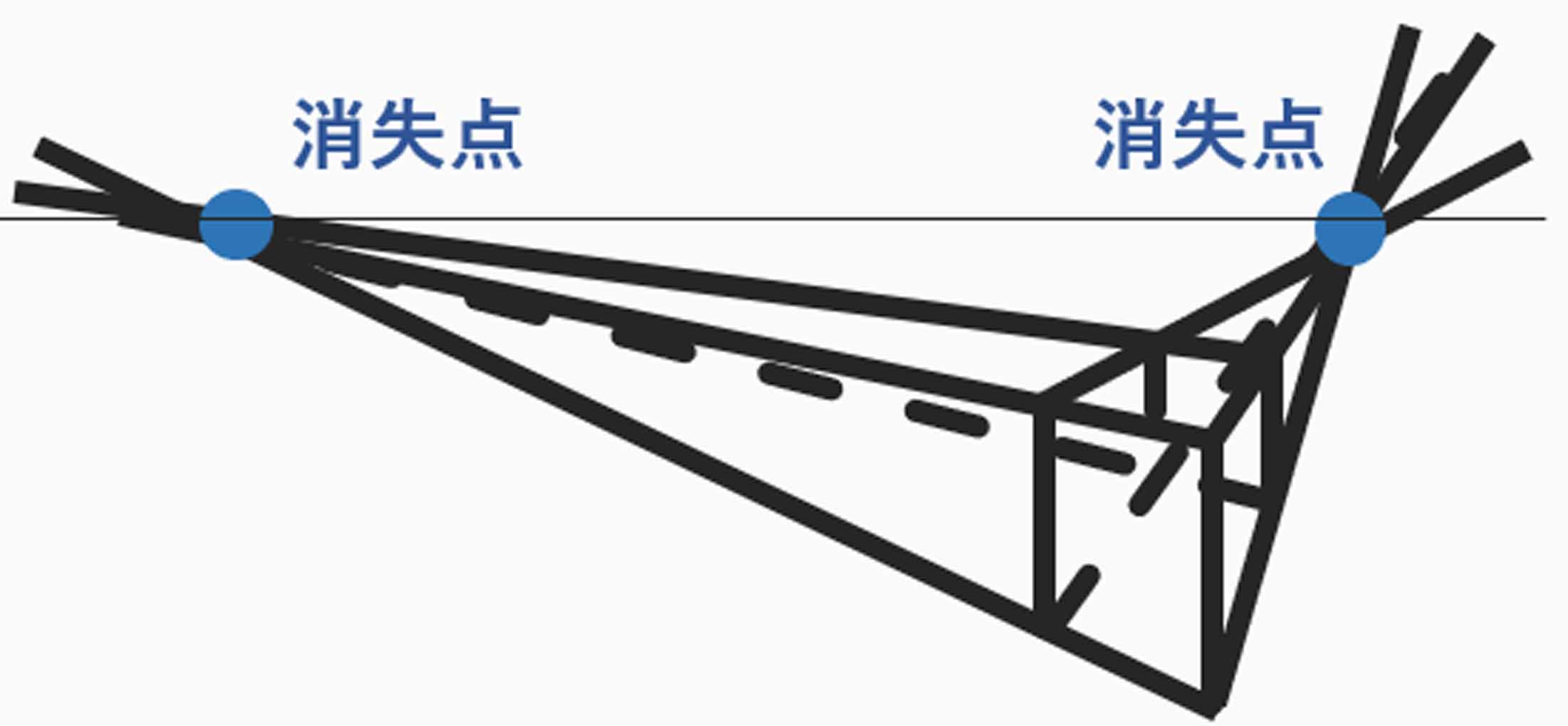
機械的に角度を決めましたが、
ある程度それぞれの辺が、消失点に向かいました。
これでほぼ、どのアングルでも、パースの狂いを抑えて
立方体を描けるようになったと思います。
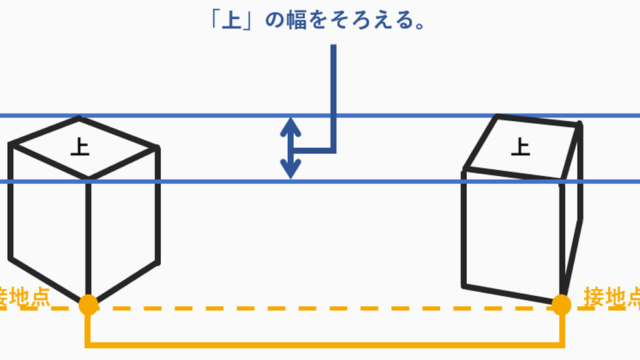
【必読5】では、今までだいたいで決めていた
立方体の幅を、簡単に、ほぼ正確に決められる方法を
ご紹介いたします。
それではご精読ありがとうございました!