こんにちはカクシュウです!
【必読4】では、【必読3】の方法では、描けないアングルになったときの、
対処方法をご紹介致しました。
【必読4】【必読3】の補足です!→これで立方体のパースは大丈夫!|角度でわかる!二点透視図法克服法 (kakusyu.com)
【必読5】では、立方体を描く上で皆さんも疑問に思っている、それぞれの面の
「奥行き」の決め方についてご紹介します。
2点透視図法で立法体を描いた時に
もちろん、それぞれの面の奥行きを決めなければなりません。
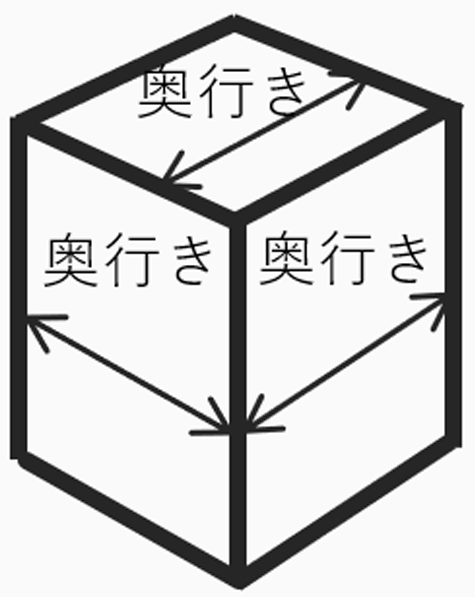
今まで皆さんは、どのように奥行きを決めていたでしょうか?
私の場合は、自分の感覚で「だいたい」で決めていました。
しかし、今回ご紹介する介線法という方法なら
ほぼ正確に奥行きを決めることが出来ます。
どうしてほぼ正確なのかは、後ほど説明致します。
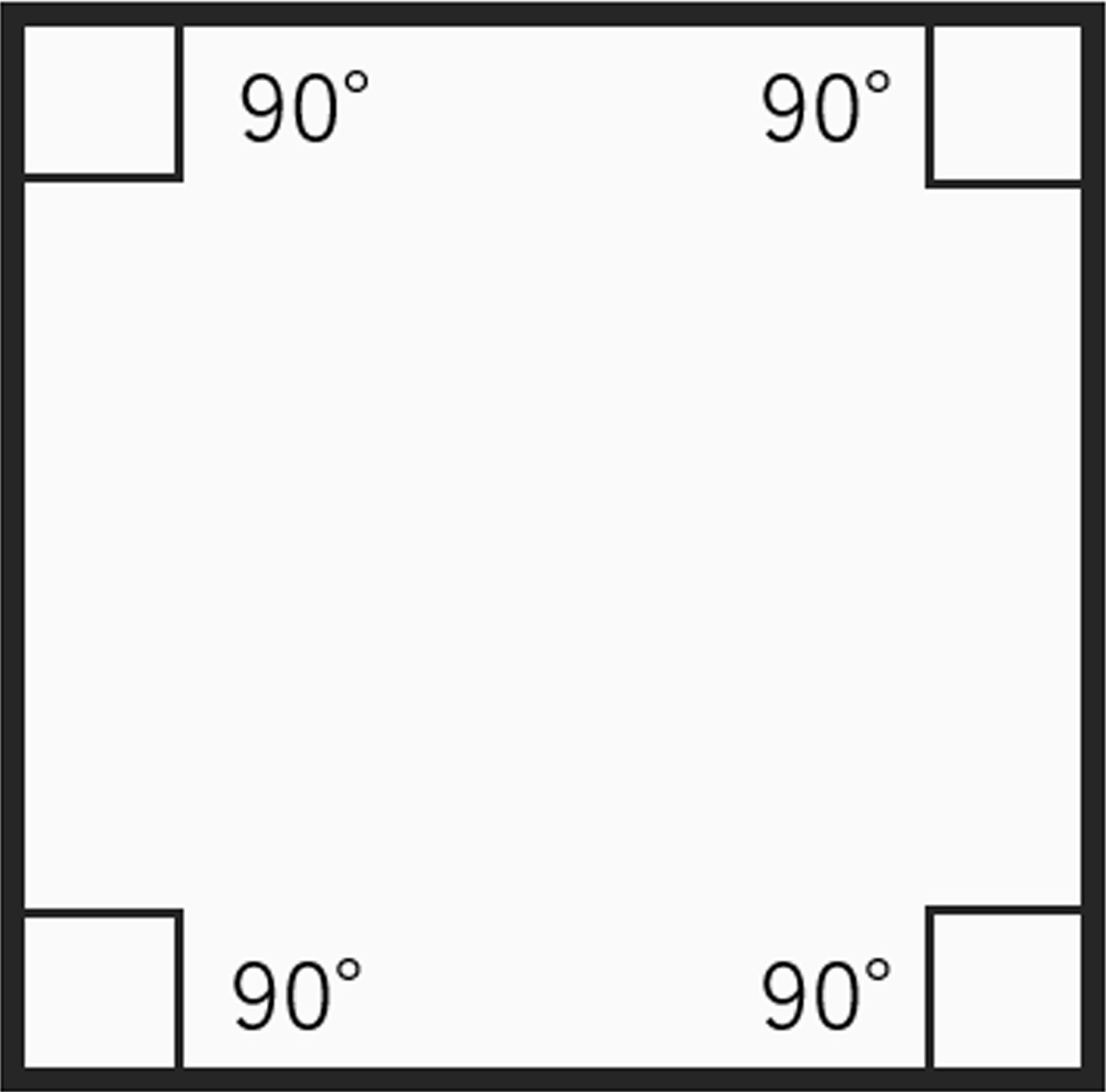
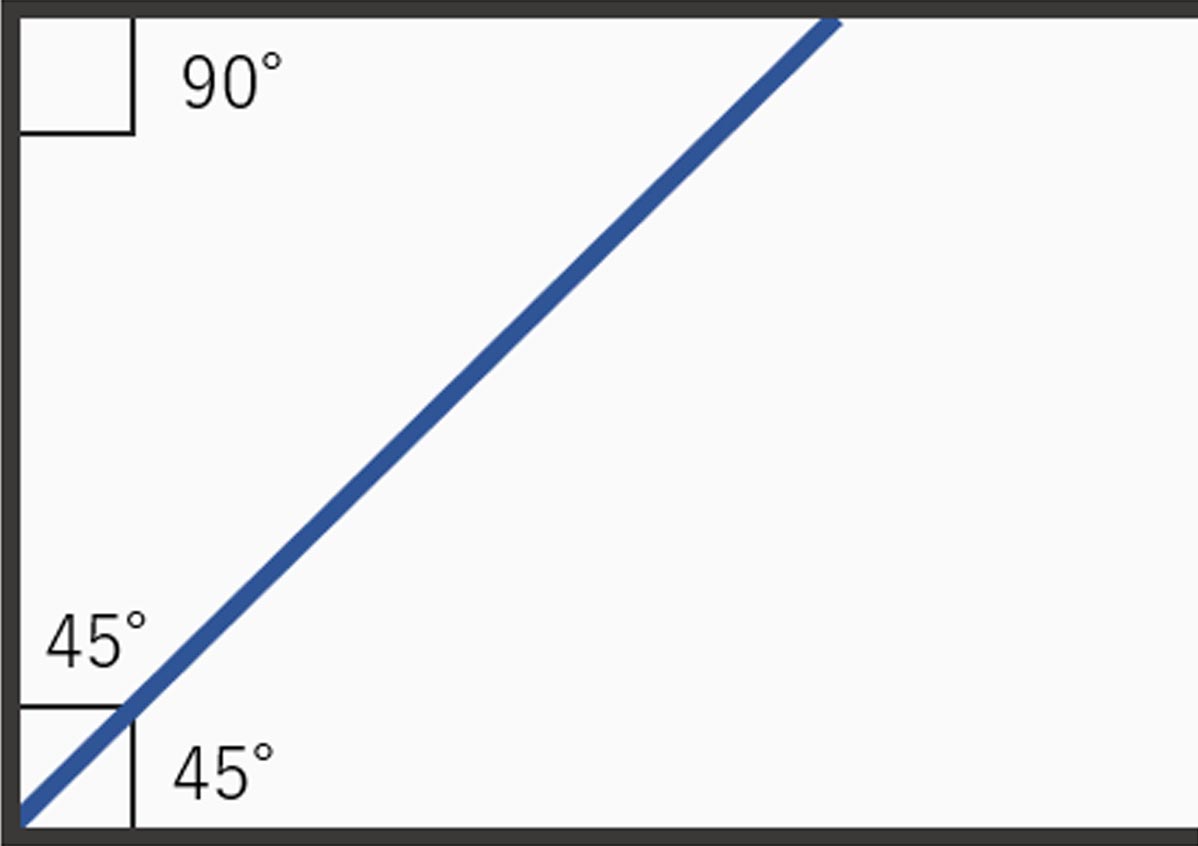
立方体というのは、6面全てが下記の様に
正方形になっています。
当たり前ですが、4辺全て90°になります。
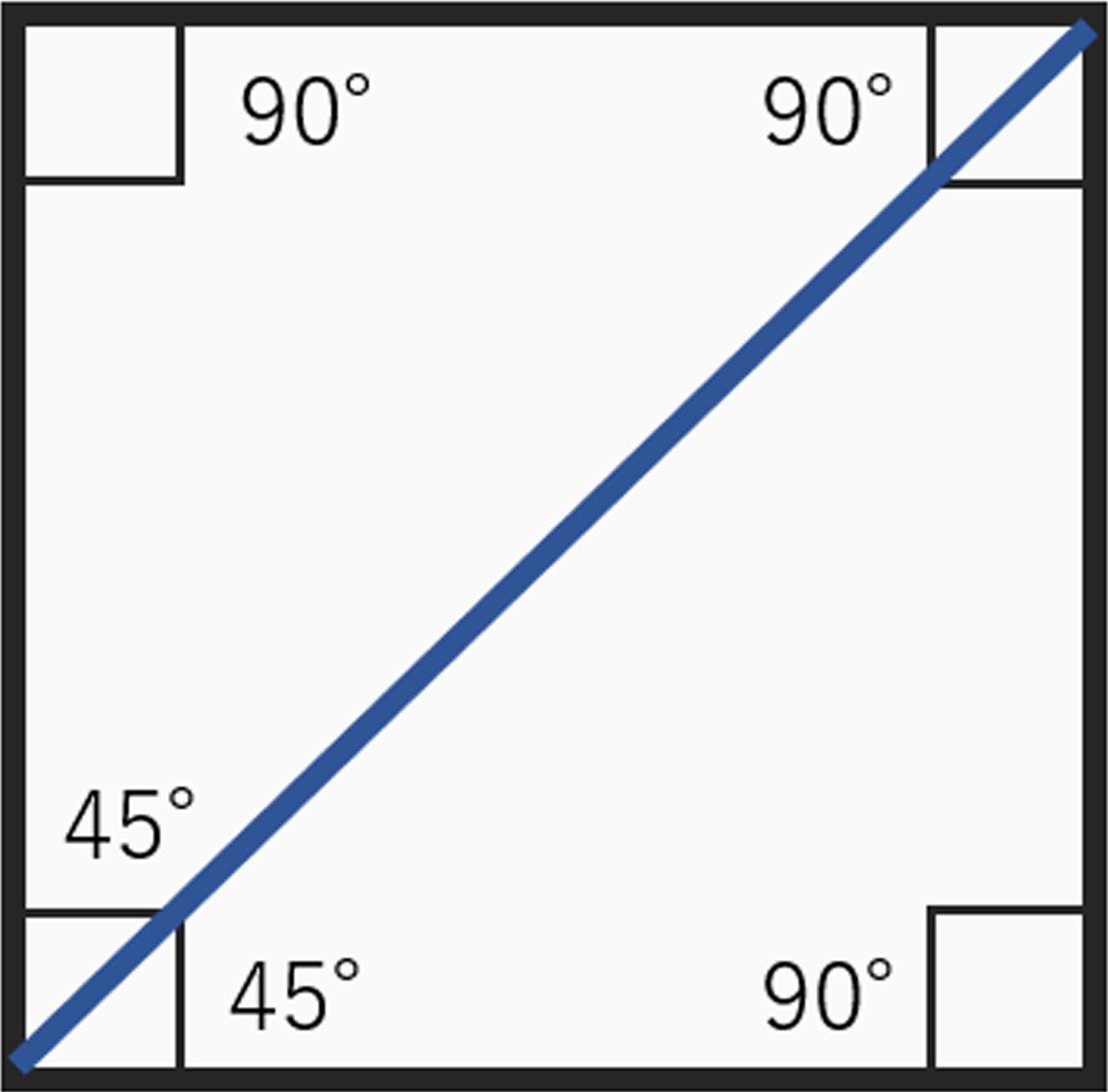
それでは、この正方形に対角線を引いてみましょう。
正方形の場合、対角線を引くと下図の様に、
90°の角度を2分割して45°の角度が2つ出来ます。
これは、対角線でもあり、90°を2分割する
2等分線でもあります。またこの2等分線を
引けば奥行きが決まります。
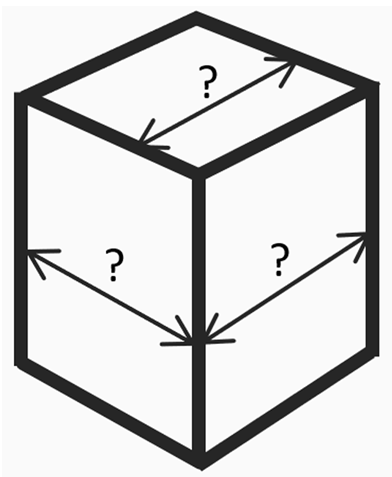
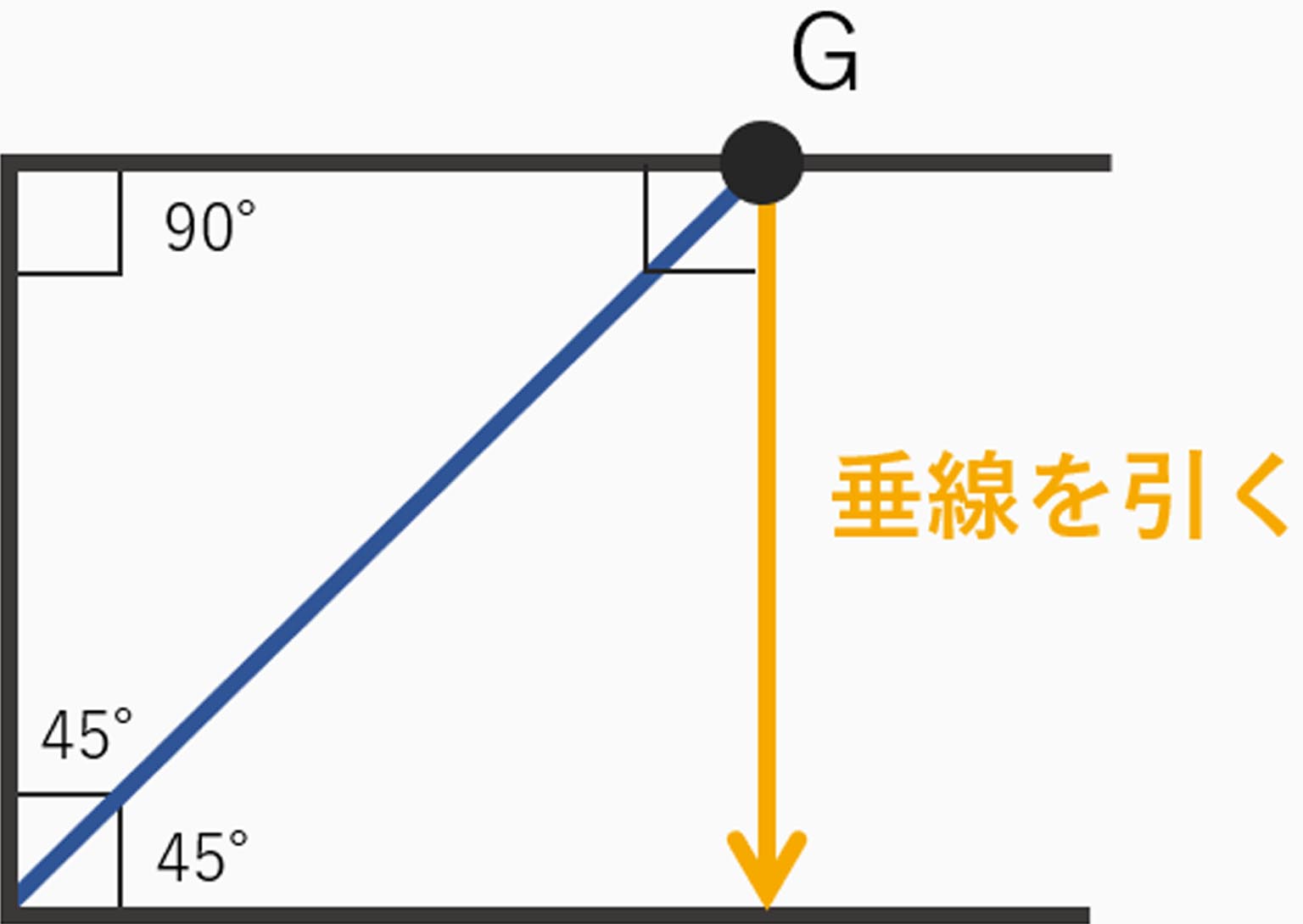
どういうことかと言いますと、例えば下記の様に
一辺が決まっていない状態で2等分線を引きます
次に2等分線と辺の交点Gから垂直に線を引きます。
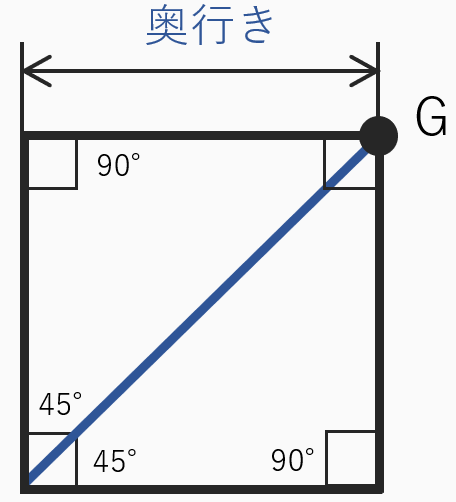
この2等分線を引くと自動的に4辺の長さ即ち奥行きがわかります。
パースで形が歪んでいても、全ての面は正方形であることに
変わりはないので、
2等分線を引けば、ほぼ正確に奥行きを求めることが出来ます。
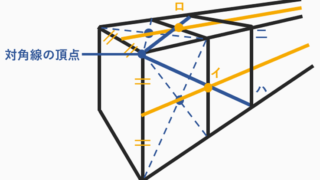
試しに、2点透視図法で描かれている立方体で
奥行きを求めてみましょう!
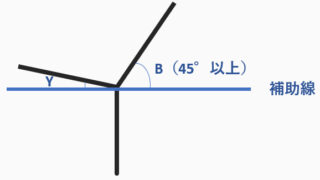
下図のように角α、角βをだいたい2分割する様な
線を引きます。
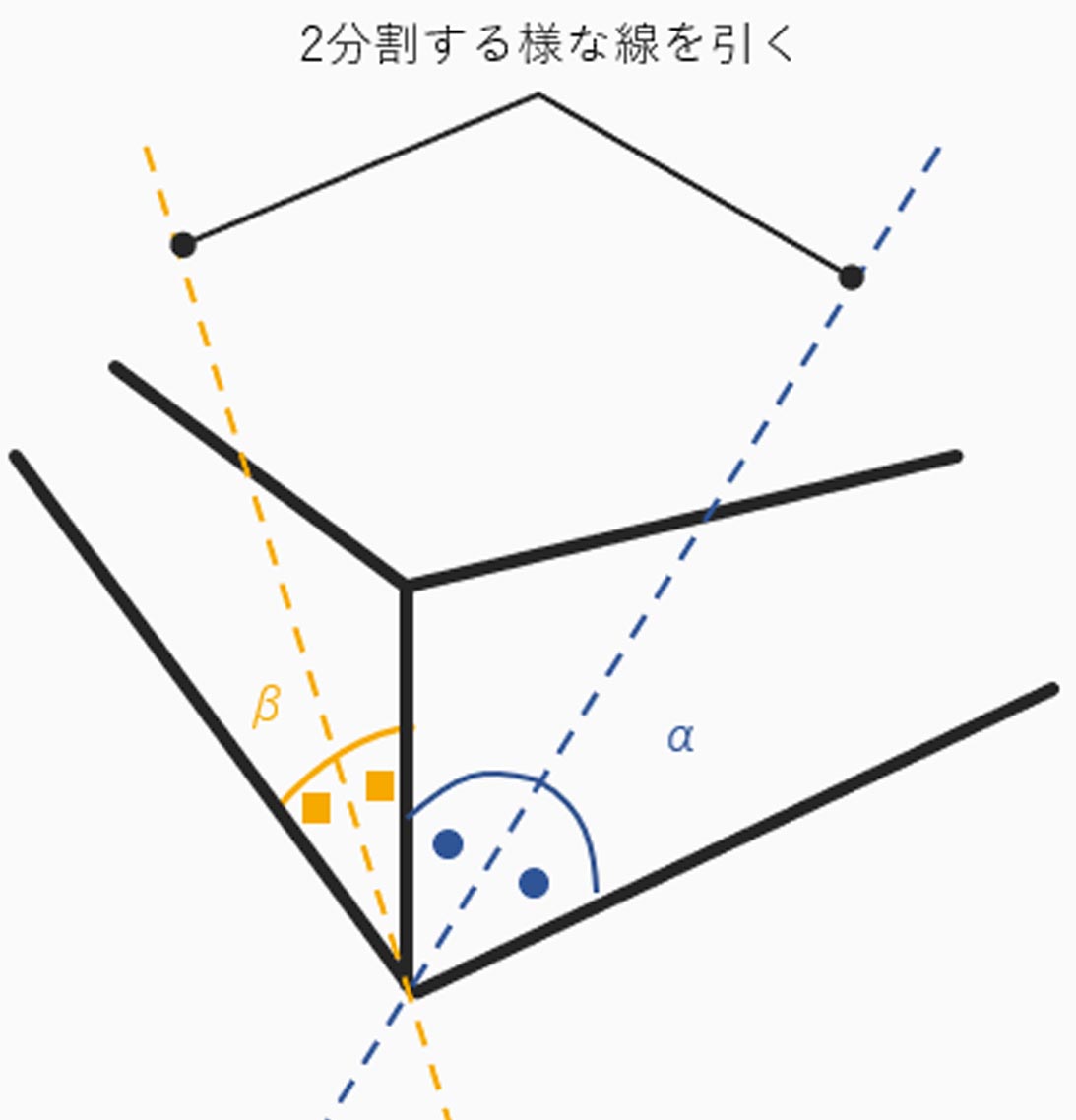
次に2等分線と辺の交点H、Iから補助線と直角になるように、垂直線を引きます。
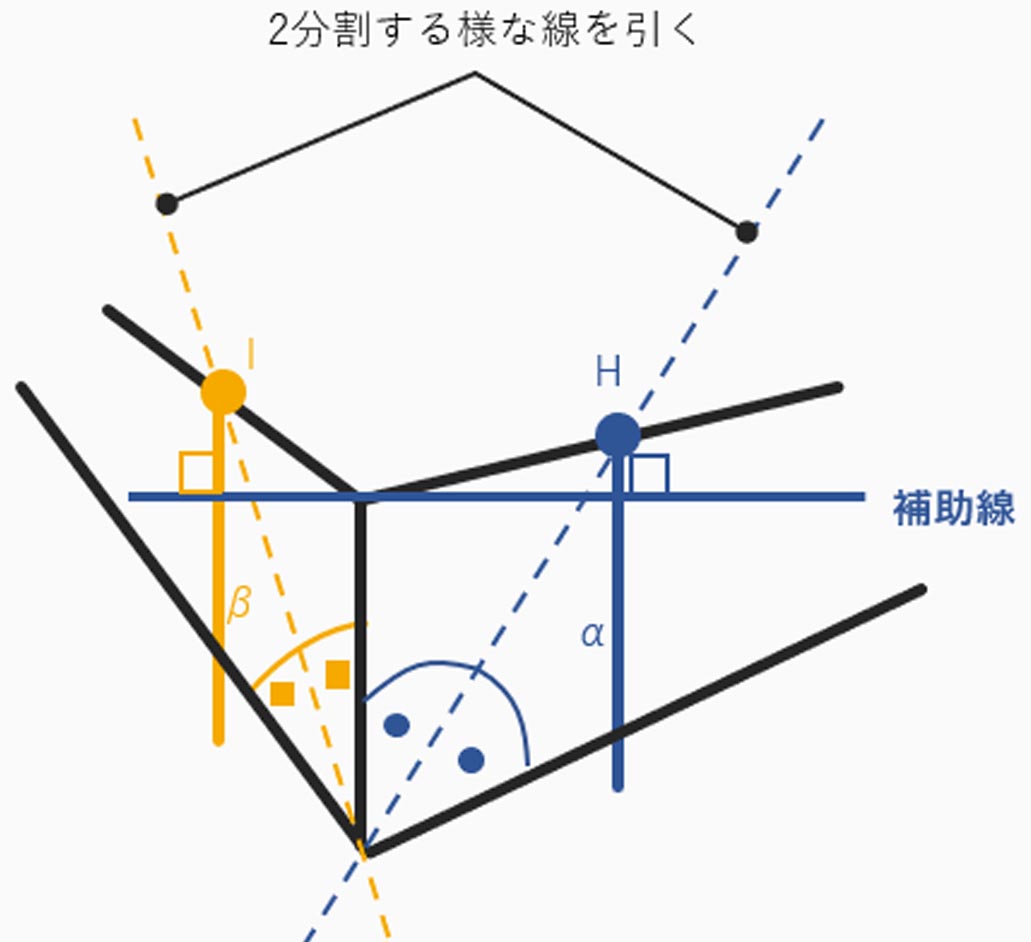
図で示した垂直線と辺の長さがまさしく
「奥行き」を表します。
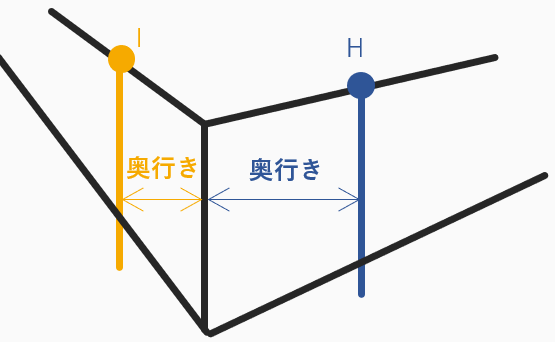
この2つの奥行きが決まれば、
【必読3】の角度の関係を満たせば、
他の辺の奥行きも自動的に決まります。
【必読3】画面外に消失点があるとパースが狂ってしまう!→角度の関係に気づけば描けます!|角度でわかる!二点透視図法克服法 (kakusyu.com)
しかし、この方法は冒頭でお話したように
ほぼ正確な方法です。
では、理論的に正しく決めた奥行きと
どの位、誤差があるのでしょうか?
実は今までお話してきたことは、
2点透視透象という、かなり時間を要する作図方法で
全て正確に作図することができます。
参考リンクをご参照下さい。
参考リンク:大阪芸術大学 図学CAD教室
下記が2点透視透象の考えで作図した
理論的に正しい立方体です。
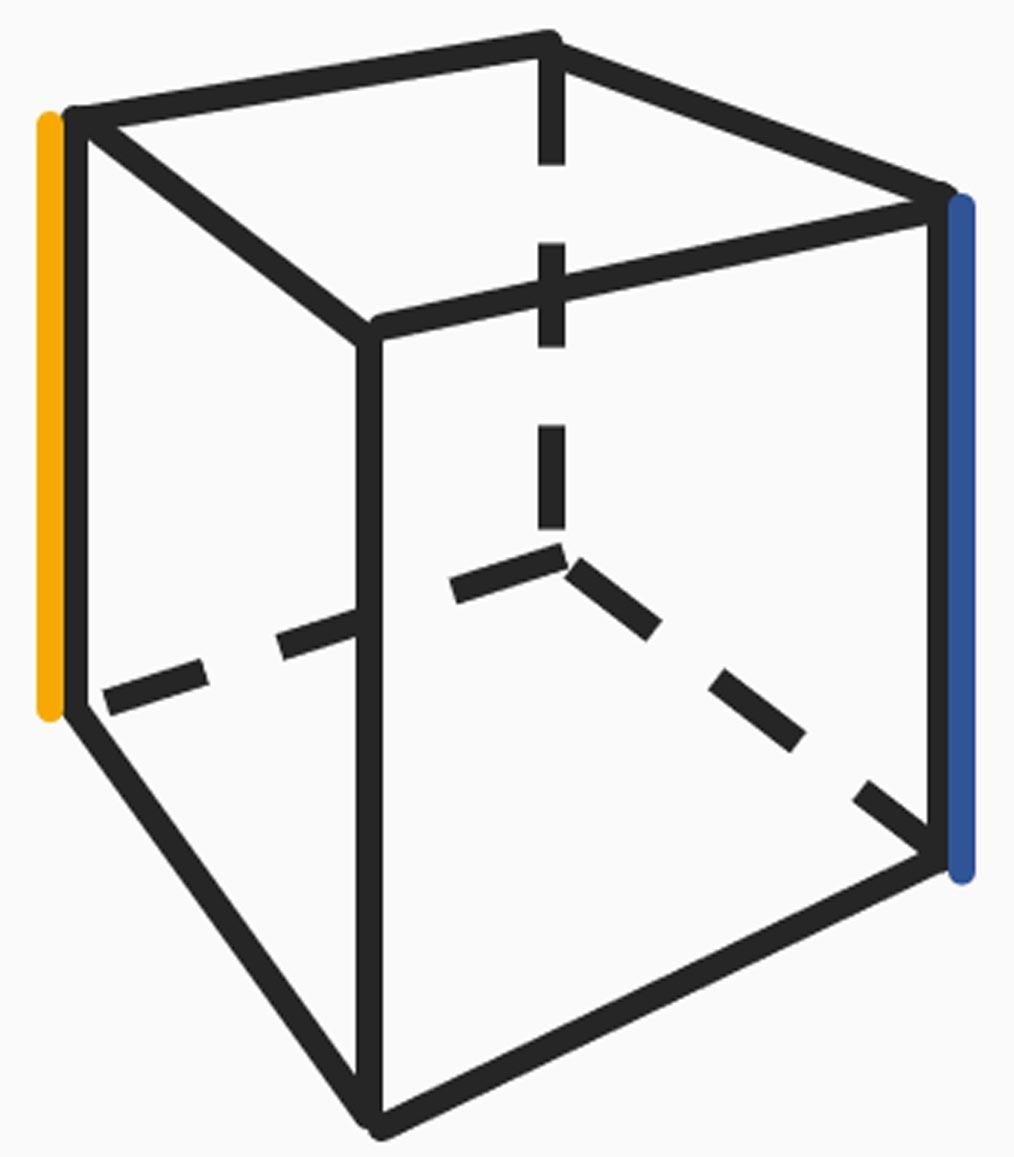
この立方体に先程、2等分線を使用して奥行きを決めた箇所を
重ね合わせてみましょう。
青とオレンジ色の線が、先程作成した箇所です。
ほぼ正確に、奥行きが決まっているのではないでしょうか。
冒頭でもお話しましたが、どうして「ほぼ正確」に
なってしまうかと申しますと、当たり前の話に
なってしまうのですが、下図のように4辺の長さが同じで、
向かい合う辺が平行であれば、対角線=2等分線になるのですが
パースがきいた歪んだ形状では、対角線=二等分線にはならないからです。
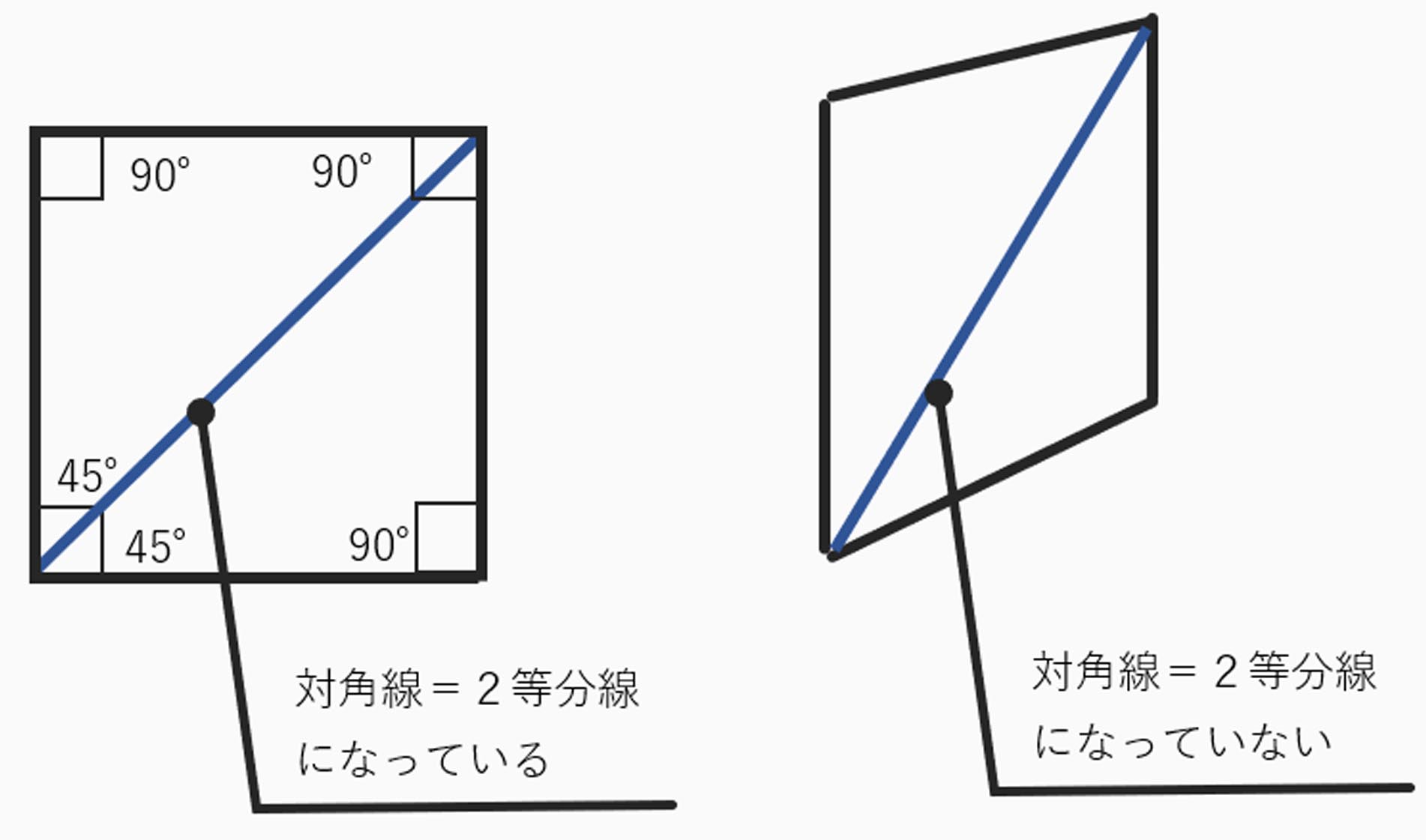
しかし完全でなくても、2等分線にかなり近い関係にはなっているので、
漠然と奥行きをきめるよりは、かなり正確に求めることができます。
もちろんおよそで、幅を決めているので、
奥行きが「少し広いな」「少し狭いな」と感じる事もあります。
そこはご自身の感覚で、作成した奥行きに対して微調整する
のもよろしいかと思います。
以上【必読1】~【必読5】までかなりの反則技の数々でしたが、
2点透視図法で立方体を描くコツを紹介しました。
この立方体を描ければ、皆さんが描きたい物の数が
かなり増えると思います。
それではご精読ありがとうございました!